QHack 2023: 4 week prep challenge, day 10, A topology survey

I continued on the Algorithm track with the adapting topologies exercise. It is an easy, but very enjoyable task, I just really like working with graphs.

Topology

Quanta need to be next to each other, when performing multi-qubit operations like CNOT, SWAP, etc. on them. If you want to perform a multi-qubit operation on non-adjacent qubits, you’ve got to SWAP them around, until they are next to each other. Therefore, a higher connectivity is beneficial to save up coherence for the main calculations.

However, operations on qubits may cause cross-talk on neighboring qubits, and therefore reducing coherence.

Now the topology of a QPU has to weigh-in both effects, and there are topologies that optimize for reduced cross-talk (e.g. ion traps), maximal connectivity, or seek to balance the two (e.g. IBM’s heavy hexagonal lattice).

Exercise

Now in this exercise, a toy topology is provided, and the challenge is to calculate the number of SWAPs required to perform a CNOT gate. For this, I used the python library networkx.

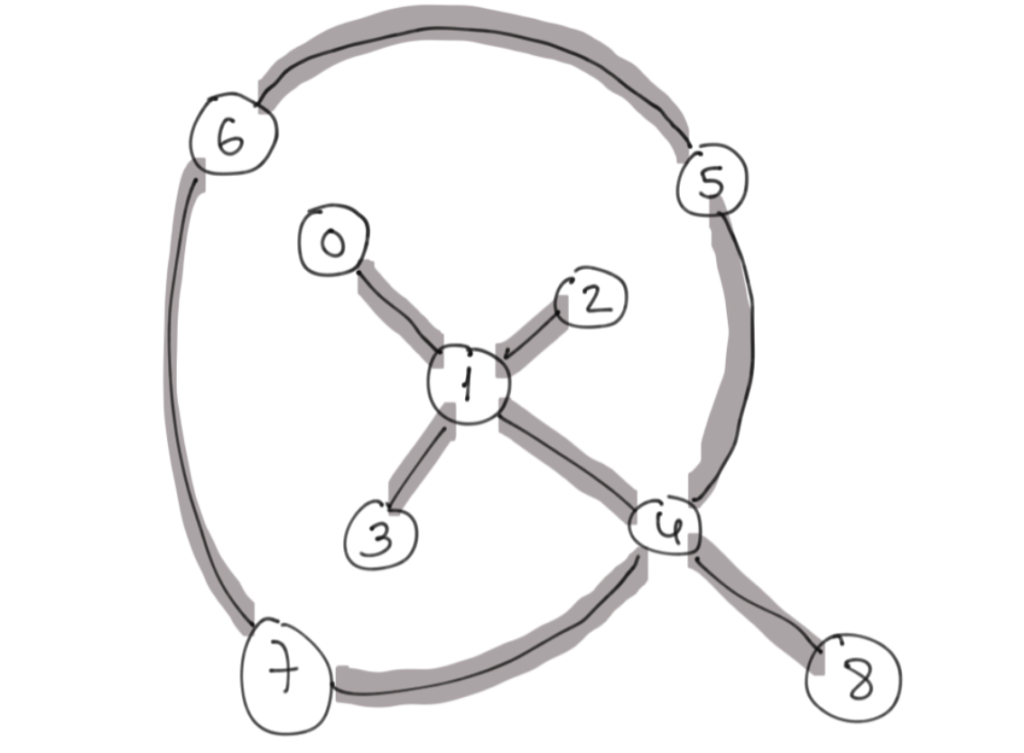
import networkx as nx

def get_topology_graph():
    """Create an adjacency graph, of the topology dict.
    
    Args:
    
    Returns: 
        - (nx.Graph): adjacency graph
    """
    
    G = nx.Graph()
    
    for i, nodes in graph.items():
        elist = [(i, j) for j in nodes]
        G.add_edges_from(elist)
    
    return G

The SWAP count, is then easily calculated from the length of the shortest path (don’t forget to rewind the operations, to clean up after the CNOT).

def n_swaps(cnot):
    """Count the minimum number of swaps needed to create the equivalent CNOT.

    Args:
        - cnot (qml.Operation): A CNOT gate that needs to be implemented on the hardware
        You can find out the wires on which an operator works by asking for the 'wires' attribute: 'cnot.wires'

    Returns:
        - (int): minimum number of swaps
    """
    
    G = get_topology_graph()
    wires = cnot.wires
    path = nx.shortest_path(G, wires[0], wires[1])
    
    return 2*(len(path)-2)

The results check out, success!

Plotting a sample circuit

To round the story up, I wrote a small routine to build out a circuit, that actually swaps the qubits around ..

dev = qml.device("default.qubit", wires=len(graph))

@qml.qnode(dev)
def n_swaps_perf(wire1, wire2):
    G = get_topology_graph()
    
    path = nx.shortest_path(G, wire1, wire2)
    path.pop(-1) # remove last item, to have easier indexing in loops
    
    for i in range(1, len(path)):
        qml.SWAP(wires=[path[i], path[i-1]])
        
    qml.CNOT(wires=[path[-1], wire2])
    
    rev_path = list(reversed(path))
    
    for i in range(1, len(rev_path)):
        qml.SWAP(wires=[rev_path[i], rev_path[i-1]])
        
    return qml.expval(qml.PauliZ(wires=wire2))

.. and plots the resulting circuit.

drawer = qml.draw(n_swaps_perf)
print(drawer(8,2))

1: ───────╭SWAP─╭●─╭SWAP───────┤     
2: ───────│────╰X─│───────────┤  <Z>
4: ─╭SWAP─-╰SWAP────╰SWAP─╭SWAP─-┤     
8: ─╰SWAP────────────────╰SWAP─┤     

Looks good.