QHack 2023: 4 week prep challenge, day 15, SWAP Test

I did another basic exercise on the QML track, but honestly, I was struggling a lot with this one. The hard-earned victories are both satisfying and instructive. But first a quick outline of the exercise.

The challenge was to estimate the inner product of two feature vectors. A distance measure is derived from this quantity and is used to perform a k-NN (k-nearest neighbor) algorithm – in this configuration an artificial use case.

The inner product can be estimated with the SWAP-test.

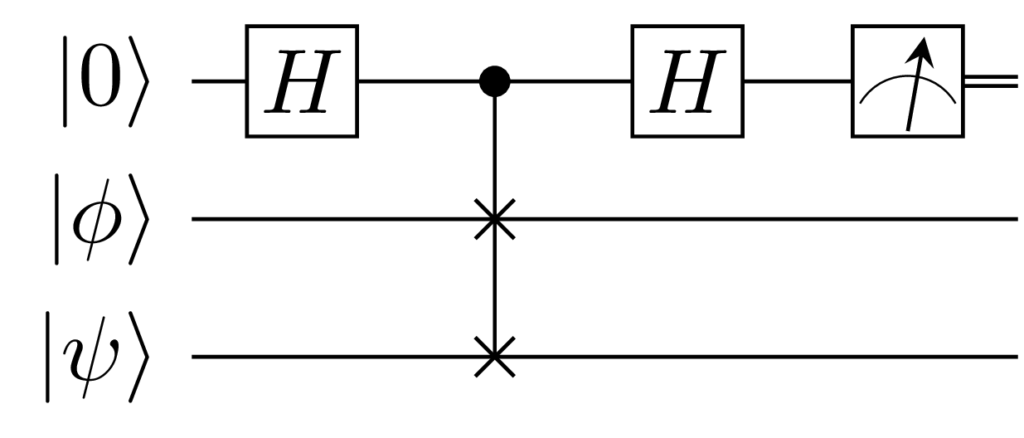
SWAP test circuit, taken from Wikipedia.

The inner product estimate is calculated from

\[ P(\text{control qubit} = 0) = \frac{1}{2} + \frac{1}{2}\lvert\langle \psi | \phi \rangle\rvert^2 \]

Implementation

In this implementation, each feature vector is normalized, and since each vector has dimension two, a single qubit suffices to encode the data.

from pennylane import numpy as np
import pennylane as qml


def distance(A, B):
    """Function that returns the distance between two vectors.

    Args:
        - A (list[int]): person's information: [age, minutes spent watching TV].
        - B (list[int]): person's information: [age, minutes spent watching TV].

    Returns:
        - (float): distance between the two feature vectors.
    """

    def prep_state():
        """Function that encodes the two 2D feature vectors into the amplitudes of one qubit each."""
        
        tan_thetaA = A[0]/A[1]
        thetaA = np.arctan(tan_thetaA)
        tan_thetaB = B[0]/B[1]
        thetaB = np.arctan(tan_thetaB)
        
        qml.RY(2.*thetaA, wires=0)
        qml.RY(2.*thetaB, wires=1)
    
    
    dev = qml.device("default.qubit", wires=3)
    @qml.qnode(dev)
    def circuit():
        """Quantum circuit that encodes two 2D-feature vectors and performs a SWAP test.
        
        Returns:
            - ([float, float]): probabilities of states measured on the control qubit.
        """
        prep_state()
        
        qml.Hadamard(wires=2)
        qml.CSWAP(wires=range(2,-1,-1))
        qml.Hadamard(wires=2)
        
        return qml.probs(2)

    # print(qml.draw(circuit)())
    
    tmp = circuit()[0] # .5 + .5<A,B>^2
    A_times_B = np.sqrt(2.*tmp-1.)
    
    return np.sqrt(2*(1.-A_times_B))

The provided tests check out.

Lessons learned

I will seize this opportunity to reflect upon my solution strategies. The problem statement was a little less concrete than the ones of previous exercises. In the starter code two hints were pointing at the SWAP Test and the PennyLane amplitude encoding functionality. After an initial implementation failed, I did some more research and found a SWAP-test implementation on a PennyLane forum. This was more confusing then helpful, I believe the core confusion being how the normalization is done in this encoding strategy.

Anyways, the clean bottom up solution, along with some debugging print-outs eventually worked out.

Implementation

Lessons learned

Related