Tag: Cliques

I felt I had some unfinished business on yesterday’s exercise, so I drafted an improved optimization routine. I formulated an ad hoc hypothesis, that shows in a small-scale test some improvements over the original optimization scheme.

An important observation: order matters

Two measurements can be combined, if they fulfill certain criteria, cf. yesterdays post. However, if you combine measurements locally using a greedy procedure, you might end up with sub-optimal combinations, and requiring more measurements eventually.

If you number your measurements 1 .. N as nodes in a graph and edges between nodes, if you can perform them in parallel, you may end up with a graph like the following.

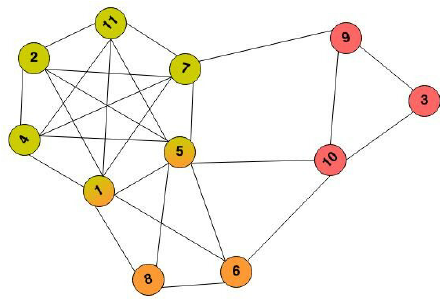
Given this graph, you immediately see a large clique (a fully connected subgraph, nodes 1, 2, 4, 5, 7, 11), that you would instinctively replace with a single measurement right away. You’d continue with the remaining cliques (3, 9, 10 and 8, 6), three measurements in total. The order of replacement is key, if by chance you’d join up the nodes 5, 6, 10 first, you’d end up with 4 measurements in total.

Create the graph

Using the networkx package, I created the aforementioned undirected graph.

import networkx as nx

def create_compatibility_graph(obs_hamiltonian):
    """Create a graph, where the nodes represent measurements and edges are formed for combinable measurments.

    Args:
        - obs_hamiltonian (list(list(str))): List of measurements (list of list of Pauli operators), e.g., [["Y", "I", "Z", "I"], ["Y", "Y", "X", "I"]].

    Returns:
        - (networkx.Graph): graph that represents the measurments and possible combinations thereof
    """
    G = nx.Graph()
    G.add_nodes_from(range(len(obs_hamiltonian)))
    
    for i in range(len(obs_hamiltonian)):
        for j in range(i):
            if check_simplification(obs_hamiltonian[i], obs_hamiltonian[j]):
                G.add_edge(i, j)
    return G

Create the optimizer

Iteratively replace cliques through combined measurements, starting from the biggest clique.

def optimize_measurement_cliques(obs_hamiltonian):
    """Create an optimized (smaller) list of measurements, based on cliques of combinable measurements. 
    Creates a graph representation of the measurements and iteratively combines cliques of measurements,
    starting from the largest.

    Args:
        - obs_hamiltonian (list(list(str))): List of measurements (list of list of Pauli operators), e.g., [["Y", "I", "Z", "I"], ["Y", "Y", "X", "I"]].

    Returns:
        - list(list(str)): an optimized list of measurements
    """
    G = create_compatibility_graph(obs_hamiltonian)
    
    result = []
    
    while True:
        cliques = nx.find_cliques(G) # TODO: this should be done only once

        cliques_list = list(cliques)
        cliques_list.sort(key=len, reverse=True)

        if not cliques_list: # no cliques left
            break
        elif len(cliques_list[0]) == 1: # only singleton cliques left
            result += [list(obs_hamiltonian[c[0]]) for c in cliques_list]
            break
        else: # optimize 
            measurement = optimize_measurements(obs_hamiltonian[cliques_list[0]])
            result += measurement
            G.remove_nodes_from(cliques_list[0])
    
    return result

Test and compare the optimizers

A small routine to create some test data,…

import numpy as np

def create_measurements(count, width):
    """Create ´count´ random measurement sequences of width ´width´.

    Args:
        - count (int): number of random measurements to create
        - width (int): number of Pauli operators per measurement

    Returns:
        - list(list(str)): list of measurements, e.g., [["Y", "I", "Z", "I"], ["Y", "Y", "X", "I"]].
    """
    paulis = np.array(['I', 'X', 'Y', 'Z'])
    
    rand = np.random.randint(0, 4, [count, width], dtype=int)
    return paulis[rand]

Running a few samples..

for width in range(3, 9):
    n_measurements = 3**width # there are up to 4**width possible distinct measurements
    data = create_measurements(n_measurements, width)
    benchmark = optimize_measurements(data)
    cliques = optimize_measurement_cliques(data)
    
    print(width, n_measurements, len(benchmark), len(cliques))

The results show a small, but measurable compression improvement on the initial greedy algorithm.

width	N	N (G.O.)	N (C.O.)	1 – N (C.O.)/N (G.O.)
3	27	12	10	0.166
4	81	32	30	0.063
5	243	83	82	0.012
6	729	216	209	0.032
7	2187	608	583	0.041
8	6561	1672	1564	0.065