Tag: complex Hamiltonians

Continuing on the quantum chemistry problem path, another entry level challenge. One takeaway from today’s exercise: when you are a beginner, you can even learn from the very easy problems. The problem posed no real challenge to solve it, but I learned how complex cost functions (a main ingredient in VQE algorithms) are computed.

Running the circuit multiple times, and doing the simple accounting tasks on the classical device – it’s so simple, of course! The Xanadu team provided a wonderful drawing as always

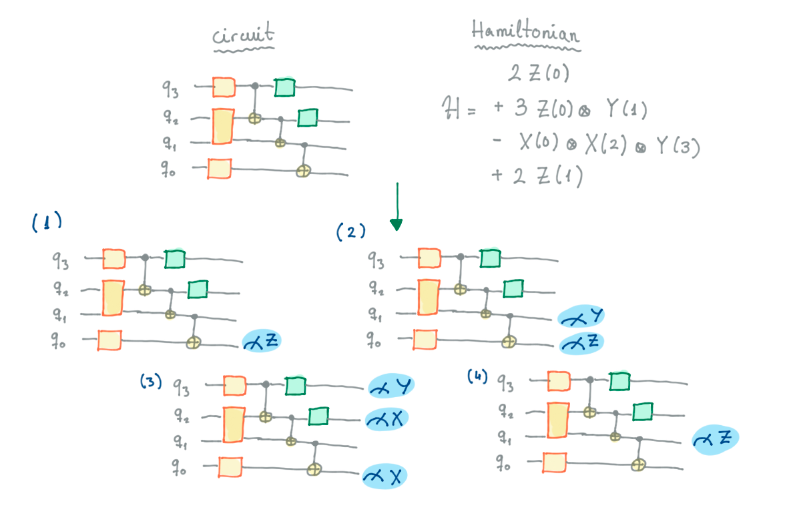
Running a quantum algorithm is costly, so you want to minimize the number of runs by combining measurements. Non-intersecting measurements, e.g. <X₁> and <Z₂> can be performed at the same time. Now this exercise asks to do just that, compress a hamiltonian with some number of additive terms into a smaller set of measurements.

A very simple greedy procedure is provided as a base. This approach is simple enough, not globally optimal, but I guess there are more advanced techniques in the Pennylane codebase.

Compression rules

Two measurements are compatible, if they either measure the same Pauli operators, or at least one of them is a null-measurement, i.e. the identity operator.

def check_simplification(op1, op2):
"""As we have seen in the problem statement, given two Pauli operators, you could obtain the expected value
of each of them by running a single circuit following the two defined rules. This function will determine whether,
given two Pauli operators, such a simplification can be produced.
Args:
    - op1 (list(str)): First Pauli word (list of Pauli operators), e.g., ["Y", "I", "Z", "I"].
    - op2 (list(str)): Second Pauli word (list of Pauli operators), e.g., ["Y", "I", "X", "I"].

Returns:
    - (bool): 'True' if we can simplify them, 'False' otherwise. For the example args above, the third qubit does not allow simplification, so the function would return `False`.
"""

result = True

for i, op in enumerate(op1):
    if op == op2[i] or op == "I" or op2[i] == "I":
        continue
    else:
        result = False
        break

return result

Compression rate

The compression rate was calculated as percentage improved over initial measurement count.

def compression_ratio(obs_hamiltonian, final_solution):
    """Function that calculates the compression ratio of the procedure.

    Args:
        - obs_hamiltonian (list(list(str))): Groups of Pauli operators making up the Hamiltonian.
        - final_solution (list(list(str))): Your final selection of observables.

    Returns:
        - (float): Compression ratio your solution.
    """

    return 1. - len(final_solution)/len(obs_hamiltonian)