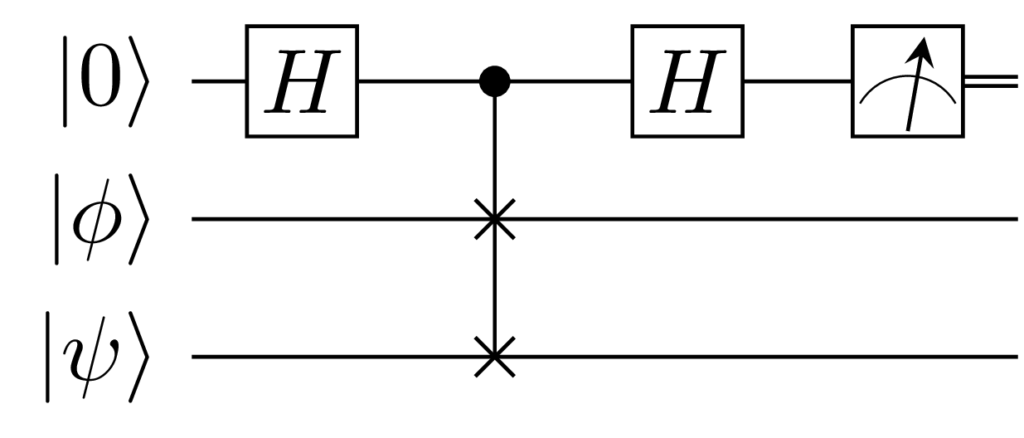
If you want to encode data in a quantum register as a uniform superposition of states, this can be done with an algorithm proposed in a very readable 2001 paper by C.A. Trugenberger.
The algorithm utilizes three registers, a processing register to load the data, a memory register, that eventually stores the target state and a two bit auxiliary register. The main idea of the algorithm is to prepare the target state in a superposition with an auxiliary bit, rotate the state into the memory state to isolate it from the following rewinding of the operations.
The implementation in PennyLane, firstly some initialization…
import pennylane as qml
from pennylane import numpy as np
data = [0,2,5]
reg_size = int(np.ceil(np.log2(np.max(data)+1)))
processing_reg = qml.wires.Wires(range(reg_size))
utility_reg = qml.wires.Wires(range(reg_size, reg_size+2))
memory_reg = qml.wires.Wires(range(reg_size+2, 2*reg_size+2))
all_wires = qml.wires.Wires.all_wires([processing_reg, utility_reg, memory_reg])
n_wires = len(all_wires)
dev = qml.device("default.qubit", wires=all_wires)Then a small helper function to encode data, into the processing register …
def load_data(n, wires=processing_reg, ctrl_wire=utility_reg[1]):
assert len(wires) == reg_size, f"wires expected a list of size {reg_size}, got {len(wires)}."
n_bin_str = np.binary_repr(n, width=reg_size)
n_bin = [int(s) for s in n_bin_str]
for i, v in enumerate(n_bin):
if v:
qml.PauliX(wires[i])Eventually the center piece
@qml.qnode(dev)
def circuit():
qml.PauliX(wires=utility_reg[1])
for m, value in enumerate(data):
# initial state |data,01,000>
load_data(value)
for i in range(reg_size):
qml.Toffoli(wires=[processing_reg[i], utility_reg[1], memory_reg[i]])
for i in range(reg_size):
qml.CNOT(wires=[processing_reg[i], memory_reg[i]])
qml.PauliX(wires=memory_reg[i])
qml.MultiControlledX(control_wires=memory_reg, wires=[utility_reg[0]])
mu = len(data) - m
angle = np.pi if mu == 1 else 2.*np.arctan(-np.sqrt(1/(mu-1)))
qml.CRY(angle, wires=utility_reg)
qml.MultiControlledX(control_wires=memory_reg, wires=[utility_reg[0]])
for i in range(reg_size):
qml.CNOT(wires=[processing_reg[i], memory_reg[i]])
qml.PauliX(wires=memory_reg[i])
for i in range(reg_size):
qml.Toffoli(wires=[processing_reg[i], utility_reg[1], memory_reg[i]])
load_data(value)
return qml.probs(wires=memory_reg)The algorithm creates correct uniform superpositions for different input data-sets.
Retrieving data, will be the next step.